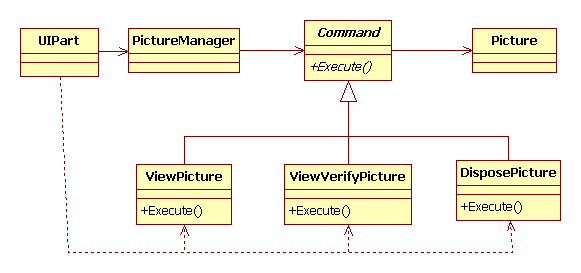
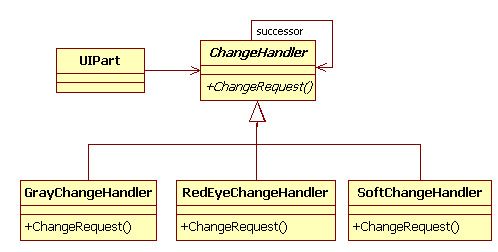
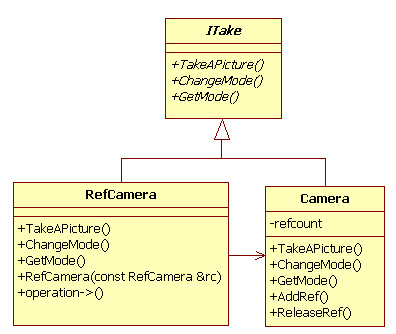
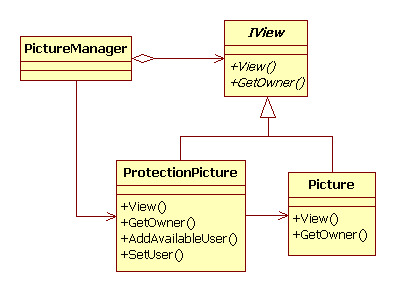
17. 명령 패턴(Command Pattern) 17.1 개요 프로그래밍하다 보면 명령을 내리는 개체와 명령을 수행하는 개체를 나누는 작업은 매 번 있는 작업입니다. 그런데 실제 요청한 작업을 수행하는 개체에서 수행에 필요한 알고리즘을 모두 포함하였을 때 비슷한 형태의 여러 메서드를 구현해야 하는 경우가 발생합니다. 경우에 따라서는 명령을 내리는 시점과 실제 명령을 수행하는 시점이 다르고 다양한 설정에 따라 구체적인 수행 알고리즘이 다른 경우도 발생합니다. 이 같은 경우에 명령을 내리는 곳에서 일부 알고리즘을 정의하여 명령을 수행하는 개체의 메서드를 호출할 때 입력 인자로 전달하는 것이 더 효과적입니다. 이러한 경우에 명령 패턴을 사용합니다. 명령 패턴은 명령을 요청하는 곳에서 수행할 알고리즘을 정의하여..