언제나 휴일

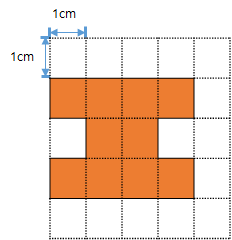
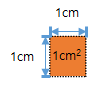
[초등 5학년 수학] 19. 넓이 구하기 - 직각으로 이루어진 도형 직각으로 이루어진 도형의 넓이 구하기 도형을 구성하는 직사각형의 넓이의 합으로 계산 도형을 먼저 직사각형으로 구분합니다. 각각의 직사각형의 넓이를 구합니다. 구한 직사각형의 넓이의 합을 구합니다. 예제 1) 다음 도형의 넓이를 구하시오. 풀이) -도형을 먼저 직사각형으로 구분합니다. -각각의 직사각형의 넓이를 구합니다. A의 넓이는 4cm2입니다. B의 넓이는 2cm2입니다. C의 넓이는 4cm2입니다. -구한 직사각형의 넓이의 합을 구합니다. 4cm2+2cm2+4cm2=10cm2 답) 10cm2 도형을 포함하는 외부 직사각형의 넓이에서 포함하지 않는 내부 직사각형의 넓이의 차로 계산 도형을 포함하는 외부 직사각형을 구합니다. 도형을 포..

[초등 5학년 수학] 18. 직사각형과 정사각형의 넓이 구하기 직사각형의 넓이 구하기직사각형의 넓이 = 가로 X 세로 A는 1cm2인 단위넓이가 가로(2) X 세로(3) 개수인 6개 있습니다. 따라서 넓이는 6cm2입니다.B는 1cm2인 단위넓이가 가로(4) X 세로(3) 개수인 12개 있습니다. 따라서 넓이는 12cm2입니다. 정사각형의 넓이 구하기정사각형은 가로와 세로의 길이가 같은 직사각형입니다. 따라서 정사각형의 넓이는 한 변의 길이를 곱한 값입니다.정사각형의 넓이 = 한 변의 길이 X 한 변의 길이 A는 한 변의 길이가 3cm 입니다. 그리고 1cm2인 단위넓이가 3 X 3 개수인 9개 있습니다. 따라서 넓이는 9cm2입니다.B는 한 변의 길이가 4cm 입니다. 그리고 1cm2인 단위넓이가 4 ..

[초등 5학년 수학] 단위넓이(1제곱센티미터, 1제곱미터) 단위넓이기준으로 사용하는 넓이를 단위넓이라 부릅니다.단위넓이에 따라 측정 값이 달라집니다.넓이를 비교할 때는 같은 단위넓이를 사용해야 합니다. 1cm2한 변의 길이가 １cm인 정사각형의 넓이１제곱센티미터라고 읽습니다． 단위넓이를 이용하여 도형 넓이 비교하기도형 A는 단위넓이 1cm2가 ９개입니다． 따라서 넓이는 9cm2입니다．도형 B는 단위넓이 1cm2가 12개입니다． 따라서 넓이는 12cm2입니다．도형 B가 도형 A보다 3cm2가 더 넓습니다． 1m2한 변의 길이가 １m인 정사각형의 넓이1제곱미터라고 읽습니다． 1cm2와 1m2 관계1m는 100cm입니다．따라서 1m2는 100cm X 100cm = 10000cm2 입니다．

[초등 5학년 수학] 직사각형 및 정사각형의 둘레 구하기직사각형사각형의 네 내각 크기가 모두 같은 사각형을 직사각형이라고 말합니다． 정사각형직사각형 중에 네 변의 길이도 모두 같은 사각형을 정사각형이라고 말합니다． 직사각형의 둘레 구하기직사각형의 마주보는 두 변의 길이는 같습니다． 따라서 가로의 길이와 세로의 길이를 알고 있으면 （가로의 길이 ＋ 세로의 길이）X 2 이 직사각형의 둘레입니다．가로의 길이는 3cm이고 세로의 길이가 ２cm인 직사각형의 둘레 ＝ (３+ 2 ) X 2 = 5 X 2 = 10 (cm) 정사각형의 둘레 구하기정사각형은 네 변의 길이가 같습니다． 따라서 한 변의 길이를 알고 있으면 한 변의 길이 X 4 결과가 정사각형의 둘레입니다． 한 변의 길이가 3cm인 정사각형의 둘레＝ ３ X ..

[초등 5학년 수학] 분수의 뺄셈분수의 뺄셈은 분모를 통분한 후에 분자끼리 빼기를 합니다． 여러 가지 방법 중에 분모의 곱을 이용하여 통분하는 것과 분모의 최소공배수로 통분하는 것을 많이 사용합니다. 분모의 곱을 이용하여 통분하면 계산하는 것이 간단해요. 분모의 최소공배수로 통분하면 비교적 분자의 크기가 작아서 뺄셈이 간단해요. 기약 분수일 때 가분수로 변경하여 계산하면 간편합니다． 계산 후에 가분수는 기약 분수로 변경해 주어야겠죠．

14. 분수의 덧셈 분수의 덧셈은 분모를 통분한 후에 분자끼리 더해요. 여러 가지 방법 중에 분모의 곱을 이용하여 통분하는 것과 분모의 최소공배수로 통분하는 것을 많이 사용합니다. 분모의 곱을 이용하여 통분하면 계산하는 것이 간단해요. 분모의 최소공배수로 통분하면 비교적 분자의 크기가 작아서 덧셈이 간단해요. 덧셈 결과가 가분수일 때는 대분수로 고쳐서 표현하세요. 그리고 약분할 수 있으면 약분하세요. 자연수는 자연수끼리 더하고 분수는 분수끼리 더하세요. 물론, 더한 결과가 가분수일 때는 자연수에 더해야겠죠. 관련 게시글 [초등 5학년 수학] 크기가 같은 분수 [초등 5학년 수학] 약분 [초등 5학년 수학] 통분

1３. 통분 통분 두 개 이상의 분수의 분모를 같게 만드는 것을 통분한다고 말합니다. *통분하기 위해서는 분모에 특정 수를 곱하거나 나누어 분모를 공배수로 만들어야 합니다. *분모를 최소공배수로 만들면 통분하기 쉽습니다. 분수의 크기 비교 통분한 후에 분자의 크기를 비교합니다.

12. 약분 약분 분모와 분자를 공약수로 나누어 간단히 표현하는 것을 약분한다고 말합니다. *공약수는 분모와 분자를 나눌 수 있는 수입니다. 기약분수 분모와 분자의 공약수가 1뿐인 분수 *기약분수는 더 이상 간단하게 표현할 수 없습니다. *분모와 분자의 최대공약수로 나누어 약분하면 기약분수를 만들 수 있습니다. 관련 게시글 [초등 5학년 수학] 크기가 같은 분수 [초등 5학년 수학] 통분

11. 크기가 같은 분수 사각형을 이용하여 분수의 크기 비교하기 같은 크기의 사각형을 분모의 개수로 칸을 나누고 분자만큼 칠하여 크기를 비교합니다． 원을 이용하여 분수의 크기 비교하기 원을 분모의 개수로 칸을 나누고 분자만큼 칠하여 크기를 비교합니다． 곱하기를 이용하여 크기가 같은 분수 만들기 분모와 분자에 0이 아닌 같은 수를 곱하면 크기가 같습니다. 나누기를 이용하여 크기가 같은 분수 만들기 분모와 분자에 0이 아닌 같은 수를 나누면 크기가 같습니다. 관련 게시글 [초등 5학년 수학] 약분 [초등 5학년 수학] 통분

10. 직육면체의 특징 서로 마주보는 면 면ㄱㄴㄷㄹ과 면ㅁㅂㅅㅇ은 서로 마주보는 면입니다. 면ㄱㄴㅂㅁ과 면ㄹㄷㅅㅇ은 서로 마주보는 면입니다. 면ㄴㅂㅅㄷ과 면 ㄱㅁㅇㄹ은 서로 마주보는 면입니다. 서로 마주 보는 면은 평행하며 합동입니다. 직육면체의 한 꼭지점에서 만나는 면은 모두 3개이며 수직으로 만납니다. 직육면체의 한 꼭지점에서 만나는 면은 모두 3개이며 수직으로 만납니다. 꼭지점 ㄷ에서 만나는 세 면 면 ㄴㄷㅅㄷ 면 ㄱㄴㄷㄹ 면 ㄷㅅㅇㄹ 관련 게시글 [초등 5학년 수학] 직육면체 [초등 5학년 수학] 정육면체 [초등 5학년 수학] 크기가 같은 분수