언제나 휴일

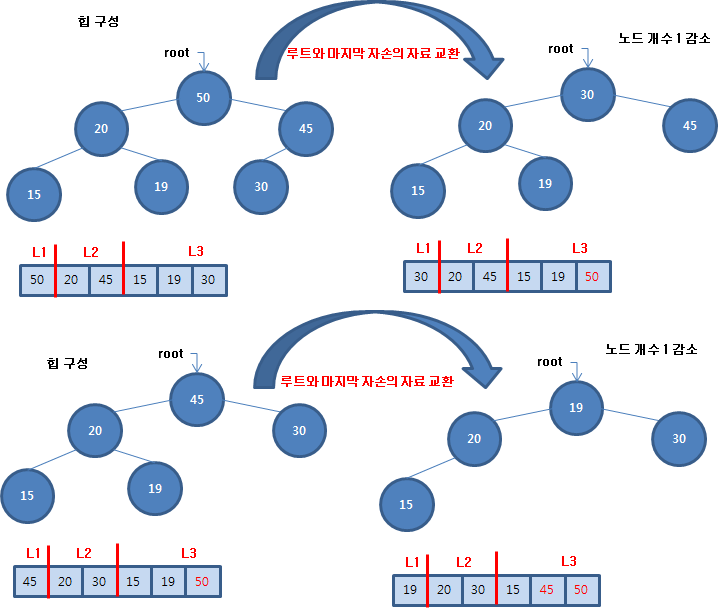
선형 자료구조에 보관한 자료 중에 최소값을 찾는 방법은 많습니다. 그 중에 분할 정복 알고리즘으로 해결하는 방법을 알아봅시다. 분할 정복 알고리즘에서는 모집합을 부분 집합으로 나누는 작업을 선행합니다. 원하는 기준에 맞게 부분 집합으로 분리한 후에 부분 집합에서 원하는 결과를 구합니다. 그리고 해결한 부분을 합쳐서 다시 커다란 집합에서 원하는 결과를 구하는 과정을 반복합니다. 최소값(최대값) 찾기 알고리즘도 분할 정복 알고리즘으로 문제를 해결할 수 있습니다. 배열의 원소 중에 최소값을 찾기 위해 원소 개수가 2보다 크면 배열의 앞 부분에서 최소값을 찾기 위해 재귀함수를 호출하고 마찬가지로 뒷 부분에서 최소값을 찾기 위해 재귀함수를 호출합니다. 그리고 배열의 앞 부분의 최소값과 뒷 부분의 최소값을 비교하여..

[C언어 알고리즘] 4. 분할정복 알고리즘 분할 정복 알고리즘은 커다란 문제를 작은 문제로 나누어 작은 문제를 해결하고 이를 다시 합쳐 커다란 문제를 해결하는 알고리즘입니다. 분할 정복 알고리즘은 내부적으로 재귀 알고리즘을 사용합니다. 대표적인 분할 정복 알고리즘에는 최소값(최대값) 찾기 알고리즘, 이진 탐색 알고리즘과 병합 정렬 알고리즘 등이 있습니다.[C언어 알고리즘] 4.1 최소값(최대값) 찾기 알고리즘[C언어 알고리즘] 4.2 이진 탐색 알고리즘[C언어 알고리즘] 4.3 병합 정렬(Merge Sort) 알고리즘

[C언어 알고리즘] 3.5.4 힙 정렬 알고리즘 소스 코드//힙 정렬 #include #define SWAP(a,b) {int t; t = a; a=b; b=t;}//a와 b를 교환 #define LCHILD(me) (2*me +1) #define RCHILD(me) (LCHILD(me)+1) #define PARENT(me) ((me-1)/2) void ViewArr(int *arr, int n); void HeapSort(int *base, size_t n); int main(void) { int arr[10] = { 9,4,3,10,5,8,7,6,2,1 }; ViewArr(arr, 10); HeapSort(arr, 10); ViewArr(arr, 10); return 0; } void HeapSor..

[C언어 알고리즘] 3.5.3 힙 정렬 알고리즘 구현 이번에는 힙 정렬 알고리즘을 구현해 보기로 해요. 힙 정렬(base:배열의 시작 주소, n: 원소 개수, compare:비교 논리) 초기 힙 구성 루트와 맨 마지막 자손 교환 n을 1 감소 반복(n: n->1) 힙 구성 루트와 맨 마지막 자손 교환 n을 1 감소 초기 힙 구성(base:배열의 시작 주소, n: 원소 개수, compare:비교 논리) 반복(i:1->n) j:=1 반복(j>0) pa:=PARENT(j) 조건: compare(base[j], base[pa])이 0보다 크면 base[j], base[pa] 교환 j: = pa 아니면 내부 루프 탈출 힙 구성(base:배열의 시작 주소, n: 원소 개수, compare:비교 논리) 반복 lc:=..

[C언어 알고리즘] 3.5.2 힙 정렬 알고리즘 성능 분석 이번에는 힙 정렬 알고리즘의 수행 속도를 계산해 보기로 해요. 힙 정렬(base:배열의 시작 주소, n: 원소 개수, compare:비교 논리) 초기 힙 구성 루트와 맨 마지막 자손 교환 n을 1 감소 반복(n: n->1) 힙 구성 루트와 맨 마지막 자손 교환 n을 1 감소 힙 정렬 알고리즘 수행 속도는 초기 힙 구성과 힙 구성을 n-1번 수행하는 비용의 합입니다. 수행 속도 = 초기 힙 구성 속도 + 힙 구성 속도 * (n-1) 초기 힙 구성(base:배열의 시작 주소, n: 원소 개수, compare:비교 논리) 반복(i:1->n) j:=1 반복(j>0) pa:=PARENT(j) 조건: compare(base[j], base[pa])이 0보다..

[C언어 알고리즘] 3.5.1 힙 정렬 알고리즘 소개 힙 정렬은 힙 트리를 이용하는 알고리즘입니다. 최대 힙을 사용하면 크기 순(Ascend)으로 정렬하고 최소 힙을 사용하면 크기 역순(Descend)으로 정렬합니다. 힙 정렬은 먼저 힙 트리를 구성합니다. 그리고 루트의 값과 맨 마지막 값을 교환한 후에 정렬 범위를 1 줄입니다. 이와 같은 작업을 반복하여 정렬 범위가 1일 때까지 반복합니다. 최대 힙 트리에서 루트는 최대 값을 갖습니다. 따라서 마지막 값과 교환하면 제일 큰 값이 맨 뒤로 배치할 수 있습니다. 그리고 난 후에 정렬 범위를 줄여나가면 최종적으로 정렬 상태를 만들 수 있는 것입니다. 힙 정렬(base:배열의 시작 주소, n: 원소 개수, compare:비교 논리) 초기 힙 구성 루트와 맨 ..

[C언어 알고리즘] 3.5 힙 정렬(Heap Sort) 알고리즘 이제 힙 정렬 알고리즘을 살펴보기로 해요. 힙 정렬은 완전 이진 트리의 한 종류인 힙 트리를 이용하여 정렬하는 알고리즘입니다. 먼저 힙 트리가 무엇인지 살펴본 후에 힙 정렬 알고리즘을 알아보고 분석 및 구현해 봅시다. 힙 트리는 부모의 값이 자식의 값보다 큰 값을 보장하는 최대 힙과 작은 값을 보장하는 최소 힙이 있습니다. 최대 힙으로 표현한 힙 트리의 루트에는 가장 큰 값을 갖고 최소 힙으로 표현하면 가장 작은 값을 갖습니다. [그림 3.12] 힙 트리 힙 트리처럼 완전 이진 트리는 배열로 많이 표현합니다. 완전 이진 트리가 아닌 이진 트리도 배열로 표현할 수 있지만 트리의 높이가 높아지고 한 쪽으로 기울어질 수록 비어있는 공간이 많아져서..

[C언어 알고리즘] 3.4.4 이진 탐색 트리 소스 코드 테스트 로직을 구현합시다. 테스트 로직은 단순히 이진 탐색 트리를 생성한 후에 다양한 도서 정보를 추가하고 검색과 삭제 기능 등을 호출하여 잘 동작하는지 확인하는 것입니다. 이 부분에 관한 별도의 설명은 생략할게요. //common.h #pragma once //헤더 파일을 한 번만 포함해서 컴파일 #include #include #include #include #include #include #include #pragma warning(disable:4996) //4996컴파일 경고 메시지 출력 해제 //Book.h #pragma once #include "common.h" #define MAX_TIT_LEN 200 #define MAX_AUT_..

[C언어 알고리즘] 3.4.3 이진 탐색 트리 구현 이제 이진 탐색 트리를 구현합시다. 이진 탐색 트리는 자료를 보관하는 컬렉션 중에 탐색 효율성을 높인 자료구조입니다. 여기에서는 도서를 보관하는 이진 탐색 트리를 구현하기로 할게요. 먼저 노드를 정의합시다. 이진 탐색 트리의 노드는 데이터와 왼쪽 자식 노드의 위치, 오른쪽 자식 노드의 위치로 구성합니다. 이 책에서는 삭제 편의성을 위해 부모 노드의 위치도 포함할게요. 그리고 동적으로 노드를 생성하는 함수를 제공합시다. typedef struct _Node Node; struct _Node { Book *book; Node *lch; Node *rch; Node *pa; }; Node *New_Node(Book *data); 이진 탐색 트리에는 root ..

[C언어 알고리즘] 3.4.2 이진 탐색 트리(Binary Search Tree)이번에는 재귀 알고리즘으로 구현하는 이진 탐색 트리(Binary Search Tree)를 알아봅시다. 이진 탐색 트리는 검색 효율을 높이기 위해 만들어진 이진 트리입니다. 이진 탐색 트리에서는 자료를 보관할 때 부모보다 작은 값을 갖는 자료는 부모의 왼쪽 서브 트리에 매달고 큰 값을 갖는 자료는 부모의 오른쪽 서브 트리에 매다는 이진 트리입니다. 그리고 이진 탐색 트리에서는 같은 값을 갖는 자료는 보관하지 않습니다. 이처럼 매달면 서브 트리도 이진 탐색 트리인 특징을 갖습니다. binary search tree = { root, sub trees} sub tree is binary search tree, left son’ s..