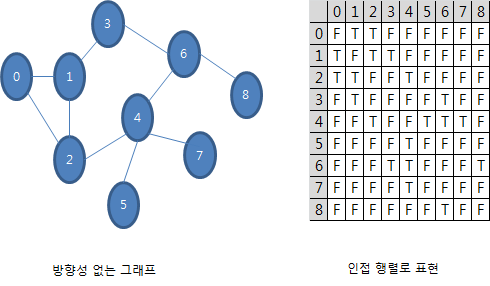
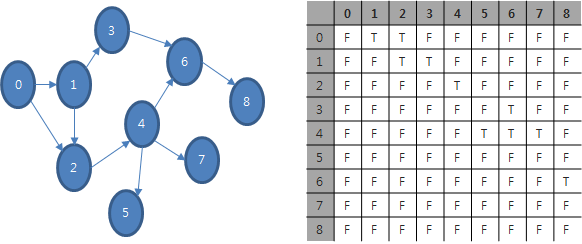
[C언어 알고리즘] 5.1.1 인접 행렬로 방향성 없는 그래프 소스 코드//방향성 없는 그래프 #include #include #include typedef struct{//그래프 형식 정의 int vn; //정점 개수 int **matrix;//그래프 인접 행렬 }Graph; Graph *MakeGraph();//그래프 만들기 void ViewNeighbors(Graph *g);//이웃 정점 보여주기 void DeleteGraph(Graph *graph);//그래프 소멸 int main(void) { Graph *graph; graph = MakeGraph();//그래프 만들기 ViewNeighbors(graph); //이웃 정점 보여주기 DeleteGRaph(graph);//그래프 소멸 return ..