언제나 휴일

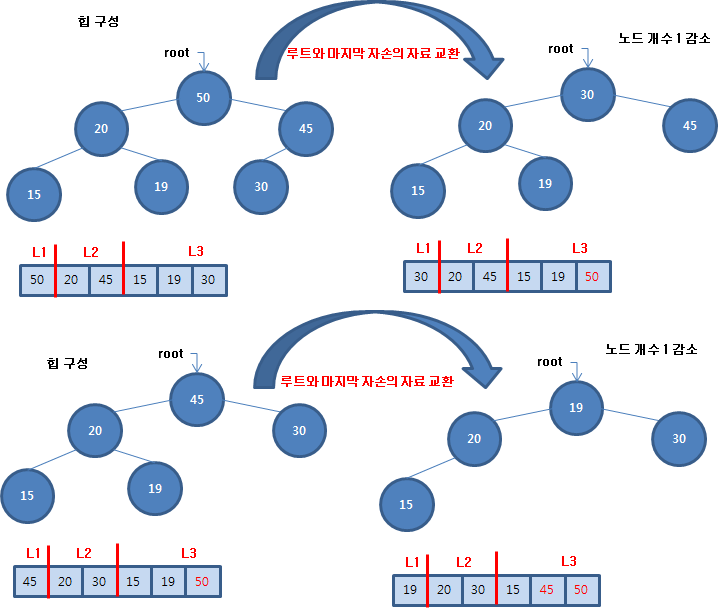
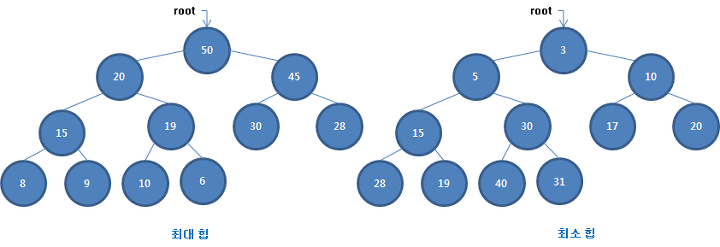
[C언어 알고리즘] 3.5.4 힙 정렬 알고리즘 소스 코드//힙 정렬 #include #define SWAP(a,b) {int t; t = a; a=b; b=t;}//a와 b를 교환 #define LCHILD(me) (2*me +1) #define RCHILD(me) (LCHILD(me)+1) #define PARENT(me) ((me-1)/2) void ViewArr(int *arr, int n); void HeapSort(int *base, size_t n); int main(void) { int arr[10] = { 9,4,3,10,5,8,7,6,2,1 }; ViewArr(arr, 10); HeapSort(arr, 10); ViewArr(arr, 10); return 0; } void HeapSor..

[C언어 알고리즘] 3.5.3 힙 정렬 알고리즘 구현 이번에는 힙 정렬 알고리즘을 구현해 보기로 해요. 힙 정렬(base:배열의 시작 주소, n: 원소 개수, compare:비교 논리) 초기 힙 구성 루트와 맨 마지막 자손 교환 n을 1 감소 반복(n: n->1) 힙 구성 루트와 맨 마지막 자손 교환 n을 1 감소 초기 힙 구성(base:배열의 시작 주소, n: 원소 개수, compare:비교 논리) 반복(i:1->n) j:=1 반복(j>0) pa:=PARENT(j) 조건: compare(base[j], base[pa])이 0보다 크면 base[j], base[pa] 교환 j: = pa 아니면 내부 루프 탈출 힙 구성(base:배열의 시작 주소, n: 원소 개수, compare:비교 논리) 반복 lc:=..

[C언어 알고리즘] 3.5.2 힙 정렬 알고리즘 성능 분석 이번에는 힙 정렬 알고리즘의 수행 속도를 계산해 보기로 해요. 힙 정렬(base:배열의 시작 주소, n: 원소 개수, compare:비교 논리) 초기 힙 구성 루트와 맨 마지막 자손 교환 n을 1 감소 반복(n: n->1) 힙 구성 루트와 맨 마지막 자손 교환 n을 1 감소 힙 정렬 알고리즘 수행 속도는 초기 힙 구성과 힙 구성을 n-1번 수행하는 비용의 합입니다. 수행 속도 = 초기 힙 구성 속도 + 힙 구성 속도 * (n-1) 초기 힙 구성(base:배열의 시작 주소, n: 원소 개수, compare:비교 논리) 반복(i:1->n) j:=1 반복(j>0) pa:=PARENT(j) 조건: compare(base[j], base[pa])이 0보다..

[C언어 알고리즘] 3.5.1 힙 정렬 알고리즘 소개 힙 정렬은 힙 트리를 이용하는 알고리즘입니다. 최대 힙을 사용하면 크기 순(Ascend)으로 정렬하고 최소 힙을 사용하면 크기 역순(Descend)으로 정렬합니다. 힙 정렬은 먼저 힙 트리를 구성합니다. 그리고 루트의 값과 맨 마지막 값을 교환한 후에 정렬 범위를 1 줄입니다. 이와 같은 작업을 반복하여 정렬 범위가 1일 때까지 반복합니다. 최대 힙 트리에서 루트는 최대 값을 갖습니다. 따라서 마지막 값과 교환하면 제일 큰 값이 맨 뒤로 배치할 수 있습니다. 그리고 난 후에 정렬 범위를 줄여나가면 최종적으로 정렬 상태를 만들 수 있는 것입니다. 힙 정렬(base:배열의 시작 주소, n: 원소 개수, compare:비교 논리) 초기 힙 구성 루트와 맨 ..

[C언어 알고리즘] 3.5 힙 정렬(Heap Sort) 알고리즘 이제 힙 정렬 알고리즘을 살펴보기로 해요. 힙 정렬은 완전 이진 트리의 한 종류인 힙 트리를 이용하여 정렬하는 알고리즘입니다. 먼저 힙 트리가 무엇인지 살펴본 후에 힙 정렬 알고리즘을 알아보고 분석 및 구현해 봅시다. 힙 트리는 부모의 값이 자식의 값보다 큰 값을 보장하는 최대 힙과 작은 값을 보장하는 최소 힙이 있습니다. 최대 힙으로 표현한 힙 트리의 루트에는 가장 큰 값을 갖고 최소 힙으로 표현하면 가장 작은 값을 갖습니다. [그림 3.12] 힙 트리 힙 트리처럼 완전 이진 트리는 배열로 많이 표현합니다. 완전 이진 트리가 아닌 이진 트리도 배열로 표현할 수 있지만 트리의 높이가 높아지고 한 쪽으로 기울어질 수록 비어있는 공간이 많아져서..

9.1 힙 정렬 알고리즘이제 힙 정렬 알고리즘을 살펴보기로 해요. 힙 정렬은 완전 이진 트리의 한 종류인 힙 트리를 이용하여 정렬하는 알고리즘입니다. 먼저 힙 트리가 무엇인지 살펴본 후에 힙 정렬 알고리즘을 알아보고 분석 및 구현해 봅시다. 힙 트리는 부모의 값이 자식의 값보다 큰 값을 보장하는 최대 힙과 작은 값을 보장하는 최소 힙이 있습니다. 최대 힙으로 표현한 힙 트리의 루트에는 가장 큰 값을 갖고 최소 힙으로 표현하면 가장 작은 값을 갖습니다. 힙 트리처럼 완전 이진 트리는 배열로 많이 표현합니다. 완전 이진 트리가 아닌 이진 트리도 배열로 표현할 수 있지만 트리의 높이가 높아지고 한 쪽으로 기울어질 수록 비어있는 공간이 많아져서 메모리 효율이 떨어집니다. 하지만 완전 이진 트리는 마지막 자료가 ..