언제나 휴일

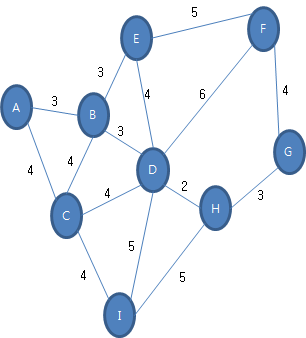
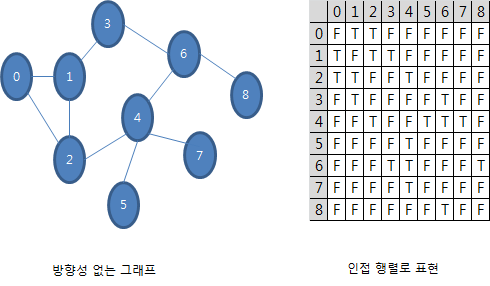
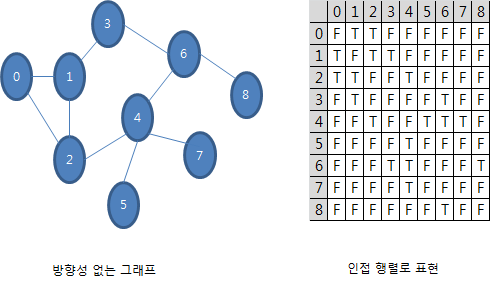
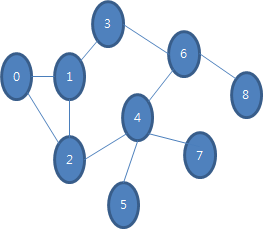
11.3.1 다익스트라 알고리즘 구현 이번에는 다익스트라 알고리즘을 구현해 보아요. 그래프와 Heuristic 부분은 깊이 우선 탐색과 너비 우선 탐색에서 구현한 것과 매우 흡사합니다. 먼저 간선 클래스를 정의합시다.class Edge{두 개의 정점과 간선의 비용이 멤버로 필요하겠죠. string vt1; string vt2; int weight;public:두 개의 정점과 간선의 비용을 입력 인자로 받게 생성자를 제공하세요. Edge(string vt1,string vt2,int height);특정 정점이 존재하는지 두 개의 정점 모두 존재하는지 판별하는 메서드를 제공하세요. bool Exist(string vt)const; bool Exist(string vt1, string vt2)const;하나의..

11.3 다익스트라 알고리즘 이번에는 간선의 비용이 있는 그래프에서 최단 거리를 찾는 알고리즘 중에 하나인 다익스트라 알고리즘을 살펴 보아요. 다익스트라 알고리즘은 출발 정점에서 가까운 경로 순으로 보관하는 우선 순위 큐와 출발 정점에서 특정 정점까지 최단 경로 후보들을 보관하는 후보 테이블을 이용하는 알고리즘입니다. 참고로 벨만 포드 알고리즘은 간선의 비용이 음수일 때도 적용할 수 있는 알고리즘이며 나머지는 다익스트라와 같습니다. 제일 먼저 출발 정점에서 인점한 정점을 방문하는 다음 경험 목록을 구합니다. 그리고 마지막 정점까지 가는 경로가 후보 테이블에 있는지 확인합니다. 만약 후보 테이블에 있는 경로가 새로운 경로보다 비용이 많으면 새로운 경로로 교체합니다. 처음 마지막 정점이 방문하였을 때는 후보..

11.2 너비 우선 탐색(정점과 간선 그래프) 이번에는 정점과 간선 집합 그래프에서 너비 우선 탐색 코드를 구현합시다. 그래프와 Heuristic, Edge에 관한 코드는 10.4 깊이 우선 탐색(정점과 간선 그래프) 코드와 같으니 참고하세요. 먼저 깊이 우선 탐색하는 순서를 이해하기 쉽게 구현한 코드를 구현합시다. int main(){먼저 그래프를 생성하고 정점과 간선을 추가하세요. Graph *graph = new Graph();//그래프 동적 생성 for(int i = 0; iAddVertex(i); } graph->AddEdge(0, 1);//간선 추가 graph->AddEdge(0, 2);//간선 추가 graph->AddEdge(1, 2);//간선 추가 graph->AddEdge(1, 3);//..

11.1 너비 우선 탐색(인접 행렬) 구현 제일 먼저 인접 행렬로 너비 우선 탐색을 구현해 보아요. 그래프와 Heuristic에 관한 코드는 10.3.3 깊이 우선 탐색(인접 행렬) 코드와 같으니 참고하세요. 먼저 깊이 우선 탐색하는 순서를 이해하기 쉽게 구현한 코드를 구현합시다. int main(){먼저 그래프를 생성하고 간선을 추가하세요. Graph *graph = new Graph(9);//그래프 동적 생성 graph->AddEdge(0, 1);//간선 추가 graph->AddEdge(0, 2);//간선 추가 graph->AddEdge(1, 2);//간선 추가 graph->AddEdge(1, 3);//간선 추가 graph->AddEdge(2, 4);//간선 추가 graph->AddEdge(3, 6)..

11. 너비 우선 탐색(Breath First Search) 이번에는 그래프에서 최단 경로를 찾는 너비 우선 탬색(Breath First Search) 알고리즘을 알아보아요. 앞에서 다룬 깊이 우선 탐색(Depth First Search)알고리즘은 그래프 상에서 두 정점 사이에 경로를 찾는 알고리즘이었습니다. 한 정점에서 갈 수 있는 다음 정점으로 이동하고 다시 다음 정점으로 이동하면서 경로를 찾는 것을 반복하였습니다. 만약 더 이상 이동할 곳이 없다면 이전에 이동했었던 곳에서 다시 찾는 형태로 경로를 찾는 알고리즘입니다. 위 그래프에서 0에서 8로 가는 정점을 예로 들어 볼게요. 여기에서는 한 정점에서 다음 정점으로 갈 때 높은 수를 갖는 정점을 우선 방문하는 예로 설명할게요. 깊이 우선 탐색 알고리즘..

10.4 깊이 우선 탐색(정점과 간선 그래프) 이번에는 그래프를 정점(Vertex)과 간선(Edge) 집합으로 표현한 후에 깊이 우선 탐색을 구현해 보아요. 먼저 간선을 정의합시다. 여기에서는 방향성 없는 그래프로 표현할게요.class Edge{간선의 두 정점을 멤버 필드로 추가하세요. int vt1; int vt2;public:생성할 때 두 개의 정점을 입력 인자로 받습니다. Edge(int vt1,int vt2);특정 점정을 포함하는지 판별하는 메서드를 제공하세요. bool Exist(int vt)const;두 개의 정점을 포함하는지 판별하는 메서드도 제공하세요. bool Exist(int vt1, int vt2)const;하나의 정점을 입력 인자로 받은 후에 나머지 정점을 반환하는 메서드도 제공하세..

10.3.3 깊이 우선 탐색(인접 행렬) 코드 다음은 앞에서 작성한 인접 행렬로 구현한 그래프와 이를 이용한 깊이 우선 탐색 소스 코드입니다. 여기에서는 방향성 없는 그래프를 소개할게요. //Graph.h#pragma once#include #include using namespace std;typedef vector Neighbors;class Graph{ const int vn;//정점의 개수 int **matrix;//인접 행렬 public: Graph(int vn); ~Graph(void); void AddEdge(int start, int goal);//간선 추가 void ViewNeighbors()const; void ViewNeighbor(int vt)const; Neighbors FindN..

10.3.2 깊이 우선 탐색(인접 행렬) 구현 이번에는 인접행렬로 구현한 그래프를 이용하여 깊이 우선 탐색 알고리즘을 구현해 봅시다. 깊이 우선 탐색은 한 정점에서 갈 수 있는 이웃 정점으로 이동한 후에 다시 이웃 정점으로 이동하는 것을 반복합니다. 단 이미 방문한 정점은 방문하지 않으면서 목적지까지 경로를 찾는 알고리즘입니다. 그런데 깊이 우선 탐색에서 이동하다가 더 이상 갈 곳이 없으면 이전 갈림길에서 다른 길을 선택할 수 있어야 합니다. 이를 위해 현재까지 이동한 경로를 경험 정보로 관리하고 한 정점에서 갈 수 있는 이웃 정점을 추가한 다음 경험 정보를 스택에 보관해 두었다가 더 이상 갈 곳이 없으면 스택에서 꺼내와서 다른 경로를 찾게 구현할 거예요. 다음은 스택을 이용한 깊이 우선 탐색 알고리즘의..

10.3.1 그래프 구현 그래프는 방향성 없는 그래프와 방향성 있는 그래프가 있습니다. 먼저 방향성 없는 그래프를 살펴보아요. 방향성 없는 그래프는 정점 A에서 정점 B로 이동할 수 있으면 언제나 정정 B에서 정정 B로 이동할 수 있음을 보장하는 그래프예요. 방향성 없는 그래프를 표현하는 방법 중에 간단한 그래프에는 인접 행렬을 많이 사용해요. 인접 행렬로 방향성 없는 그래프를 표현하면 좌상단에서 우하단으로 이어지는 대각선에 대칭 형태죠. 먼저 그래프 형식을 정의하기로 해요. 인접 행렬로 그래프를 표현할 때 그래프에는 정점 개수와 인접 행렬이 필요하겠죠. 이제 방향성 없는 그래프를 구현해 봅시다. 정점을 보관하는 벡터를 이웃이라고 정합시다.typedef vector Neighbors;class Graph..

10.3 인접 행렬을 이용한 깊이 우선 탐색 깊이 우선 탐색(Depth First Search)은 그래프의 한 정점에서 다른 정점으로 갈 수 있는 경로를 찾는 방법 중에 하나입니다. 하나의 정점에서 갈 수 있는 이웃 정점을 방문하고 다시 방문한 정점에서 이웃 정점을 방문하면서 원하는 목적 지점까지 방문하는 방법이예요. 이 때 방문했었던 정점을 다시 방문하지 말아야 합니다. 깊이 우선 탐색처럼 그래프에서 어떠한 문제를 해결하기 위해서는 그래프를 먼저 표현할 수 있어야 합니다. 정점의 개수가 비교적 적을 때는 인접행렬로 표현할 수 있습니다. 만약 정점의 개수가 많다면 인접 행렬은 이웃하지 않는 간선을 위한 영역도 포함하여 메모리 및 성능이 나빠집니다. 이럴 때는 정점과 간선의 집합으로 그래프를 표현하여 문제..