언제나 휴일

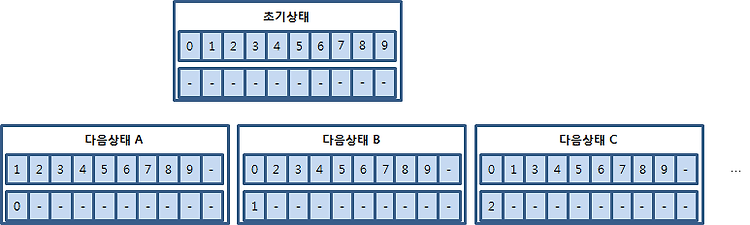
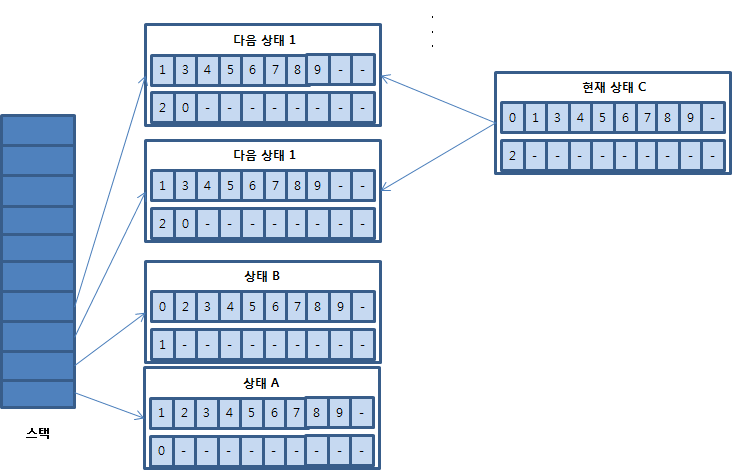
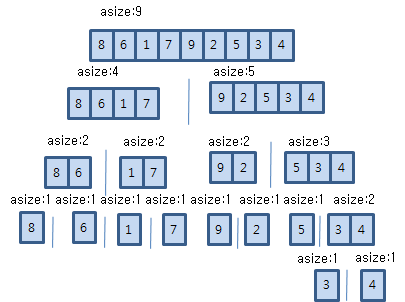
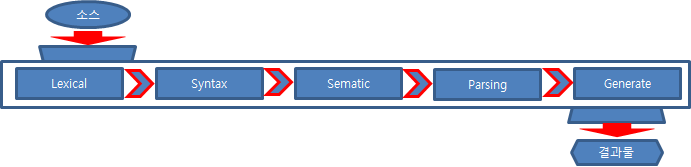
10.2.2 순열 문제 소스 코드 다음은 앞에서 작성한 순열 문제의 소스 코드입니다. //Heuristic.h#pragma once#include #include using namespace std;typedef vector Bucket;typedef Bucket::iterator BIter;typedef Bucket::const_iterator CBIter; class Heuristic;typedef vector Heues;typedef Heues::iterator HIter;typedef Heues::const_iterator CHIter; class Heuristic{ Bucket original; Bucket out;public: Heuristic(Bucket bucket); Heues EnumN..

10.2.1 순열 문제 구현 순열 문제를 구현합시다. 0~9까지 공을 보관한 초기 경험 정보를 생성스택에 보관반복(스택이 비어 있지 않다면) 스택에서 경험 정보 꺼내옮 스택에서 꺼내온 경험 정보에서 다음 경험(공을 하나 더 꺼내는) 목록 조사 반복(다음 경험 목록을 순차적으로 반복) 바구니에 공이 비면 결과 출력 그렇지 않다면 스택에 보관 먼저 공을 보관한 바구니를 공의 번호를 보관하는 벡터로 표현할게요.typedef vector Bucket;typedef Bucket::iterator BIter;typedef Bucket::const_iterator CBIter;그리고 경험 정보를 벡터에 보관한 형식을 Heues로 정의할게요.class Heuristic;typedef vector Heues;typede..

10. 2 순열 문제 바구니에 있는 여러 개의 공을 꺼내는 순서의 조합을 찾는 것은 대표적인 순열 문제입니다. 그리고 확률과 통계를 얘기할 때도 순열 문제는 자주 등장합니다. 바구니에서 공을 꺼내는 문제에서는 바구니에 남아있는 공과 꺼낸 공의 조합이 경험정보입니다. 이러한 경험 정보를 스택을 이용하여 동적 알고리즘으로 해결하면 어렵지 않게 문제를 해결할 수 있습니다. 다음은 이처럼 여러 단계로 나누어 문제를 해결하고 이전 단계에서 다음 단계로 진행할 수 있는 모든 경우의 수를 경험하는 방법으로 해결하는 동적 프로그래밍의 의사 코드입니다.초기 경험 정보를 생성스택에 보관반복(스택이 비어 있지 않다면) 스택에서 경험 정보 꺼내옮 스택에서 꺼내온 경험 정보에서 다음 경험 목록 조사 반복(다음 경험 목록을 순차..

10.1 피보나치 수열 피보나치 수열은 재귀적인 방법으로 해결하는 대표적인 알고리즘입니다. 하지만 피보나치 수열에서는 내부적으로 두 번의 재귀를 수행하여 재귀 호출 횟수는 2의 n승으로 수행 비용이 많이 들어갑니다. 만약 한 번 구한 항의 값을 기억해 두었다가 다시 호출할 때 이를 이용하면 비용은 줄어들어요. 이와 같이 경험한 정보를 이용하여 문제를 해결하는 것을 동적 프로그래밍 기법이라 말합니다. 여기에서는 피보나치 수열을 재귀적인 방법과 동적 프로그래밍 방법으로 해결하는 것을 비교해 볼게요. 다음은 피보나치 수열을 재귀적인 방법으로 구현한 코드입니다.unsigned long long Fibonacci(unsigned int n){ long long result = 1; if(n

10. 동적 프로그래밍(DYNAMIC PROGRAMMING) 커다란 문제를 여러 단계로 나누어 해결하는 알고리즘들이 있어요. 그 중에 동적 프로그래밍(Dynamic Programming)은 문제를 해결하면서 얻은 체험 정보를 이용하여 문제를 해결하는 알고리즘이예요. 동적 프로그래밍을 이용하면 한 번 해결했던 문제를 다시 해결하지 않을 수 있기 때문에 문제 해결 비용을 줄일 수 있어요. 그리고 여러 단계를 거쳐 문제를 해결하는 복잡한 문제에서 이미 수행한 정보에서 다음 단계를 해결하기 때문에 똑같은 경험을 하지 않고 모든 경우의 경험을 할 수 있어요. 물론 여러 단계로 문제를 해결해야 하는 복잡한 문제에서 모든 경우를 경험하는 것은 컴퓨터로 계산하더라도 지구가 소멸할 시기까지 계산하지 못하는 문제들도 있어..

9.4 병합 정렬(Merge Sort)이제 병합 정렬 알고리즘을 살펴보기로 해요. 병합 정렬은 배열을 분할한 후에 분할한 배열끼리 정렬하는 것을 반복하여 전체를 정렬하는 알고리즘입니다. 이처럼 커다란 문제를 작은 문제로 분할하고 분할한 작은 영역의 문제를 해결하면서 커다란 문제를 해결하는 알고리즘을 분할 정복(Divide And Conquer) 알고리즘이라고 말합니다. 먼저 분할하는 과정이 필요합니다. 분할하다가 원소의 개수가 1보다 작거나 같으면 분할은 끝납니다.조건(n

9.3 수식 파서 트리(Numeric Parser Tree)수식 계산기는 스택으로 만드는 방법과 파서 트리로 만드는 방법이 있습니다. 정규화를 할 수 있는 구문을 파싱(Parsing)할 때 파서 트리로 구현하면 운행 방법에 따라 원하는 결과물을 얻을 수 있습니다. 이번에는 컴파일러 개념을 도입한 수식 파서 트리를 만들어 보기로 할게요. 파서(Parser)는 파싱하는 도구를 말합니다. 그리고 파싱은 입력 문장을 분석하는 것을 말합니다. 따라서 파서는 입력 문장을 분석하여 원하는 결과물을 만드는 번역기라 할 수 있습니다. 컴파일러도 고급 언어로 작성한 소스를 분석하여 기계어로 번역하므로 내부에 파싱하는 파서가 필요합니다. 컴파일러가 컴파일하는 과정은 여러 단계로 나누며 컴파일러 종류에 따라 다릅니다. 여기에..

9.2 스택을 이용한 수식 파서수학에서 수식은 피연산자 사이에 연산 기호를 표기하는데 이를 중위 표기라 얘기합니다. 그런데 컴퓨터 프로그램에서 중위 표기의 수식을 계산할 때 순차적으로 수행하면 수학에서의 연산 결과가 다르게 나옵니다. 예를 들어 2+3*5의 연산은 +연산보다 *연산을 먼저하기 때문에 17이지만 순서대로 연산을 수행하면 2+3을 수행한 후에 5*5를 수행해서 25가 나옵니다. 컴퓨터 프로그램에서 제대로 수식을 계산하기 위해서는 우선 순위에 맞게 연산의 순서를 파악한 후에 계산해야 합니다. 수식을 연산 순서에 맞게 표현하는 방법 중에 연산 기호의 자식으로 피연산자를 도식하는 수식 파서 트리를 이용해서 설명해 볼게요. 2+3*5 수식에서 +연산의 피연산자는 2와 3*5의 연산 결과입니다. 그리..

9.1 힙 정렬 알고리즘이제 힙 정렬 알고리즘을 살펴보기로 해요. 힙 정렬은 완전 이진 트리의 한 종류인 힙 트리를 이용하여 정렬하는 알고리즘입니다. 먼저 힙 트리가 무엇인지 살펴본 후에 힙 정렬 알고리즘을 알아보고 분석 및 구현해 봅시다. 힙 트리는 부모의 값이 자식의 값보다 큰 값을 보장하는 최대 힙과 작은 값을 보장하는 최소 힙이 있습니다. 최대 힙으로 표현한 힙 트리의 루트에는 가장 큰 값을 갖고 최소 힙으로 표현하면 가장 작은 값을 갖습니다. 힙 트리처럼 완전 이진 트리는 배열로 많이 표현합니다. 완전 이진 트리가 아닌 이진 트리도 배열로 표현할 수 있지만 트리의 높이가 높아지고 한 쪽으로 기울어질 수록 비어있는 공간이 많아져서 메모리 효율이 떨어집니다. 하지만 완전 이진 트리는 마지막 자료가 ..

9. 기타 이진 트리 및 분할 정복 이번에는 기타 이진 트리와 분할 정복에 관해 알아봅시다. 트리는 용도에 따라 매우 다양한 형태를 지닙니다. 여기에서는 힙 정렬 알고리즘을 소개하면서 힙 트리를 다루고 수식 계산기에 사용하는 수식 파서 트리를 살펴볼게요. 그리고 문제를 분할한 후에 작은 문제를 해결하는 과정을 통해 전체 문제를 정복해 나가는 병합 정렬 알고리즘을 살펴볼 거예요. 병합 정렬 알고리즘에서 정렬할 배열을 분리하는 부분은 재귀적인 방법을 사용할 수 있어 분할 정복 알고리즘은 재귀 알고리즘으로 분류할 수 있습니다. 힙 트리는 완전 이진 트리로 노드를 이용하여 구현하는 것보다 배열을 이용하여 구현하는 것이 효과적입니다. 여기서는 자신의 부모 인덱스와 자식 인덱스를 계산할 수 있어야 하는데 이들에 대..