언제나 휴일

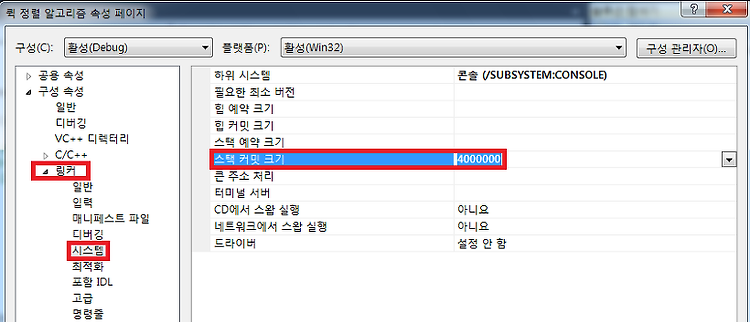
4.3.2 병합 정렬 알고리즘 구현 이제 병합 정렬 알고리즘을 구체적으로 구현합시다. #include "common.h"#include "Book.h"typedef void *Element;typedef int (*Compare)(Element , Element); void merge_sort(Element *base, int n, Compare compare){ n의 절반의 크기를 ahalf에 기억합니다. 이는 배열을 분할할 때 앞쪽 배열의 원소 개수입니다. int ahalf = n/2; 배열을 분할할 때 뒤쪽 배열의 원소 개수를 bhalf에 기억합니다. int bhalf = n - ahalf; 분할할 배열을 하나의 배열로 정복하기 위한 인덱스를 선언합니다. ai는 앞쪽 배열의 인덱스로 사용할 것이므로..

4.3 병합 정렬 알고리즘 이번에는 병합 정렬 알고리즘을 살펴봅시다. 병합 정렬 알고리즘은 배열을 작은 단위의 배열로 분할한 후에 분할한 배열을 정렬하고 이들을 다시 정렬하면서 전체 배열을 정렬하는 알고리즘입니다. 병합 정렬(base:배열의 시작 주소, n: 원소 개수, compare:비교 논리) ah:= n/2 bh:= n - ah; 조건(n이 1보다 작거나 같으면) 종료 병합정렬(base,ah,compare) 병합접열(base+ah,bh,compare) tbase에 동적 메모리 할당(원소크기*원소개수) 메모리 복사(tbase,base) ai:=0 bi:=ah i:=0 반복(ai가 ah보다 작으면서 bi가 n보다 작다) 조건(tbase[ai]가 tbase[bi]보다 작거나 같으면 base[i] := b..

4.2 이진 탐색 알고리즘 이번에는 이진 탐색 알고리즘을 알아봅시다. 이진 탐색 알고리즘은 특정 키순으로 정렬 상태의 배열에서 원하는 값의 요소를 빠르게 검색하는 알고리즘입니다. 순차적으로 비교하여 검색한다면 자료의 개수가 N개인 배열에서 최악의 경우 N번 비교해야 합니다. 하지만 이진 탐색 알고리즘으로 검색하면 logN 번이면 검색할 수 있습니다. 이진 탐색 알고리즘은 배열의 중간에 있는 요소와 비교해서 배열의 요소가 크면 재귀적으로 앞쪽 배열에서 검색하고 배열의 요소가 작으면 재귀적으로 뒤쪽 배열에서 검색합니다. 만약 같은 값이면 해당 인덱스를 반환합니다. 그리고 배열의 원소 개수가 0이면 재귀를 탈출하기 위해 인덱스 -1을 반환합니다. 이진 탐색 알고리즘(base:배열, asize:원소 개수, ke..

4. 분할 정복 알고리즘 분할 정복 알고리즘은 커다란 문제를 작은 문제로 나누어 작은 문제를 해결하고 이를 다시 합쳐 커다란 문제를 해결하는 알고리즘입니다. 분할 정복 알고리즘은 내부적으로 재귀 알고리즘을 사용합니다. 대표적인 분할 정복 알고리즘에는 최소값(최대값) 찾기 알고리즘, 이진 탐색 알고리즘과 병합 정렬 알고리즘 등이 있습니다. 4.1 최소값(최대값) 찾기 알고리즘 선형 자료구조에 보관한 자료 중에 최소값을 찾는 방법은 많습니다. 그 중에 분할 정복 알고리즘으로 해결하는 방법을 알아봅시다. 분할 정복 알고리즘에서는 모집합을 부분 집합으로 나누는 작업을 선행합니다. 원하는 기준에 맞게 부분 집합으로 분리한 후에 부분 집합에서 원하는 결과를 구합니다. 그리고 해결한 부분을 합쳐서 다시 커다란 집합에..

3.4.2 이진 탐색 트리 코드 테스트 로직을 구현합시다. 테스트 로직은 단순히 이진 탐색 트리를 생성한 후에 다양한 도서 정보를 추가하고 검색과 삭제 기능 등을 호출하여 잘 동작하는지 확인하는 것입니다. 이 부분에 관한 별도의 설명은 생략할게요. ▷BinSearchTree.h#pragma once #include "Book.h"typedef struct _Node Node;struct _Node{ Book *book; Node *lch; Node *rch; Node *pa;}; Node *New_Node(Book *data);typedef struct _BinSearchTree BST;struct _BinSearchTree{ Node *root; int count;};BST *New_BST();void..

3. 4 이진 탐색 트리 이번에는 재귀 알고리즘으로 구현하는 이진 탐색 트리를 알아봅시다. 이진 탐색 트리는 검색 효율을 높이기 위해 만들어진 트리입니다. 이진 탐색 트리는 노드와 서브 트리의 집합으로 서브 트리도 이진 탐색 트리입니다. 그리고 부모 노드는 두 개의 자식 노드를 가질 수 있고 왼쪽 서브 트리에는 부모보다 작은 값들이 오른쪽 서브 트리에는 부모보다 큰 값들이 있습니다. [그림 3.7] 이진 탐색 트리 이진 탐색 트리에서 데이터를 추가하거나 검색할 때 재귀적인 방법으로 찾을 수 있습니다. 검색 (key:키, sroot: 서브 트리의 루트노드) rkey:= sroot.key gap: = rkey - key 조건(gap IsEqual 0) sroot 반환 조건(gap < 0) 조건(sroot의 ..

3.3.2 퀵 정렬 알고리즘 구현 2 장에서 만들었던 정렬 알고리즘과 같은 방법으로 시뮬레이션 코드를 작성합니다. 여기에서는 퀵 정렬 알고리즘만 구현할게요. 참고로 퀵 정렬 알고리즘을 내부 알고리즘을 별도의 함수로 구현하지 않고 직접 구현할게요. 정렬 알고리즘은 수행 속도가 중요한 이슈이므로 복잡하더라도 하나의 함수로 구현할게요.void quick_sort(Element *base, int n, Compare compare){ 먼저 교환에 사용할 임시 변수와 피벗의 위치와 피벗보다 큰 값과 작은 값의 위치를 기억하기 위한 변수를 선언합시다. Element temp;//교환을 위한 임시 변수 int pivot = 0; //피벗의 위치를 기억하기 위한 변수 int big=0, small=0; //피벗보다 큰..

3.3 퀵 정렬 알고리즘 퀵 정렬 알고리즘은 재귀적인 방법으로 문제를 해결하는 알고리즘입니다. 퀵 정렬 알고리즘은 피벗 값을 선택하여 피벗 값보다 작은 값들은 왼쪽으로 보내고 큰 값들은 오른쪽으로 보낸 후에 이들 사이에 피벗을 위치시키는 원리를 이용합니다. 이후 피벗보다 작은 값들을 재귀 호출로 정렬하고 피벗보다 큰 값들도 재귀 호출로 정렬하는 방식입니다. 그런데 퀵 정렬은 어떠한 요소를 피벗으로 선택하냐에 따라 성능에 차이가 납니다. 만약 전체 요소의 중간 순위의 요소를 선택하면 재귀 호출에서 반씩 나누어 정렬을 하게 되어 좋은 성능을 발휘합니다. 하지만 가장 작은 값이나 가장 큰 값을 피벗으로 선택하면 최악의 성능을 발휘합니다. 여기에서는 맨 앞과 맨 뒤, 그리고 중간 위치의 요소를 비교하에 세 값 ..

3. 2 하노이 타워 재귀 알고리즘 중에 하노이 타워가 있습니다. 하노이 타워 알고리즘은 n 개의 돌을 이동시키는 문제입니다. 세 개의 기둥이 있고 하나의 기둥에 n 개의 돌이 크기 순으로 있습니다. 한 번에 하나의 돌을 이동할 수 있고 작은 돌 위에 큰 돌이 올 수 없습니다. 이와 같은 규칙을 이용하여 n 개의 돌이 있는 기둥에서 다른 기둥으로 모든 돌을 옮기는 문제입니다. [그림 3.1] 하노이 타워 이 문제를 재귀적으로 해결하면 다음과 같은 방법으로 해결할 수 있습니다. 가정: n-1개의 돌을 옮길 수 있다.가정에 의해 먼저 A에 있는 n-1개의 돌을 C를 이용하여 B로 옮깁니다.규칙에 의해 1개의 돌을 A에서 C로 옮깁니다.가정에 의해 B에 있는 n-1개의 돌을 A를 이용하여 C로 옮깁니다.따라서..

3. 재귀 알고리즘 이번에는 재귀 알고리즘을 살펴봅시다. 재귀 알고리즘은 문제를 해결하기 위해 자신의 알고리즘을 이용하여 해결하는 것을 말합니다. 수학에서 특정 명제가 참인지 증명하기 위해 명제를 이용하여 증명하는 방법과 같은 방식입니다. 예를 들어 "n!을 f(n)이라 할 때 n>1인 정수이면 n!은 n*f(n-1)이다."라는 명제를 증명하면 다음과 같이 증명할 수 있습니다. n-1일 때 위 명제가 참이라 가정하자. 가정에 의해 f(n-1) = (n-1)*(n-2)*...*3*2*1 이다.n*f(n-1) = n*(n-1)*(n-2)*...*3*2*1 = n! 이므로 위 명제는 참인 명제이다. 이처럼 자신을 이용하여 문제를 해결하는 방법을 재귀적 귀납법이라 하는데 이와 같은 방법으로 문제를 해결하는 알고..