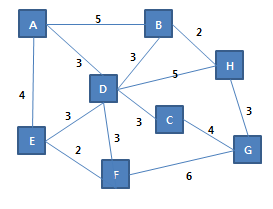
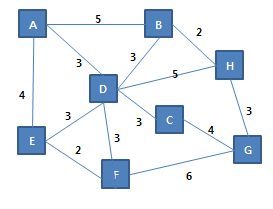
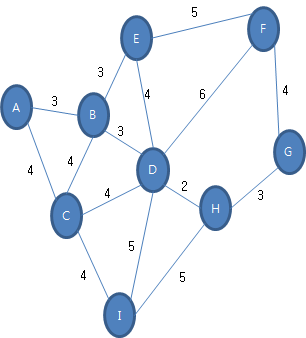
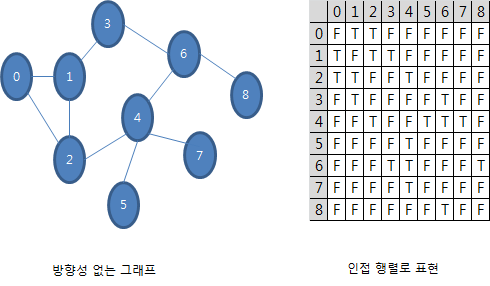
12.3.2 프림 알고리즘 소스 코드앞에서 작성한 프림 알고리즘 소스 코드입니다. //Edge.h#pragma once#include using namespace std;class Edge{ string vt1; string vt2; int weight;public: Edge(string vt1,string vt2,int height); bool Exist(string vt)const; bool Exist(string vt1, string vt2)const; string Other(string vt)const; void View()const; int GetWeight()const; string GetVt1()const; string GetVt2()const;}; //Edge.cpp#include "Edg..